Законы идеальных газов

Состояние газа определяется тремя параметрами: давлением, объемом и температурой. Для решения многих задач, возникающих при изучении газов, удобно пользоваться понятием об идеальном газе и уравнением, связываю­щим все три параметра состояния и массу газа.
Идеальными принято считать такие газы, у которых:

1. молекулы можно представить как упругие материальные частицы;
2. взаимодействие между молекулами ограничивается упругими столкновениями; 
3. пространство, занимаемое молекулами, ничтожно мало по сравнению с пространством, свободным от молекул. 

Реальные газы тем сильнее отличаются от идеальных, чем больше их плотность и ниже температура; наоборот, разрежен­ные газы, с которыми в основном имеет дело вакуумная техни­ка, по своим свойствам очень мало отличаются от идеальных.
Поэтому мы будем пользоваться уравнением состояния без всяких поправок:

(1.1)

где р — давление; V — объем; Т — абсолютная температура; N — число молекул; m — масса одной молекулы; М — масса молекулы в единицах атомного веса, т. е. число, равное его молекулярному весу; если согласно международной системе еди­ниц (СИ) за единицу массы взят килограмм, то М называется килограмммолекулой или киломолем газа (кмоль); R — газо­вая постоянная.
К уравнению (1.1) полезно сделать следующие замечания.

1. Произведение Nm выражает собой массу всего газа; если ее выразить в килограммах, то отношение Nm/M пока­зывает, сколько всего взято киломолей газа. 
2. Если газ взят в количестве одного киломоля, то Nm/M=1 и уравнение (1.1) принимает более простой вид: pV = RT. 
3. Число молекул в одном киломоле, очевидно, равно N = М/т = N_A; оно называется числом Авогадро; это число постоянно для любого вещества и равно 6,02 · 1026 кмоль^-1. Постоянство значения N_A следует хотя бы из тех соображений, что М численно равно молекулярному весу вещества, т. е. массе одной молекулы в единицах атомного веса, а т есть масса той же молекулы, но только в других единицах — килограммах. 
4. Пользуясь числом Авогадро, уравнение (1.1) можно представить в виде:

где к = R/N_A называется молекулярной газовой постоянной, или постоянной Больцмана.

1. Если в уравнениях (1.1) и (1.2) все величины выражены в единицах СИ, то газовые постоянные независимо от рода газа имеют значения:

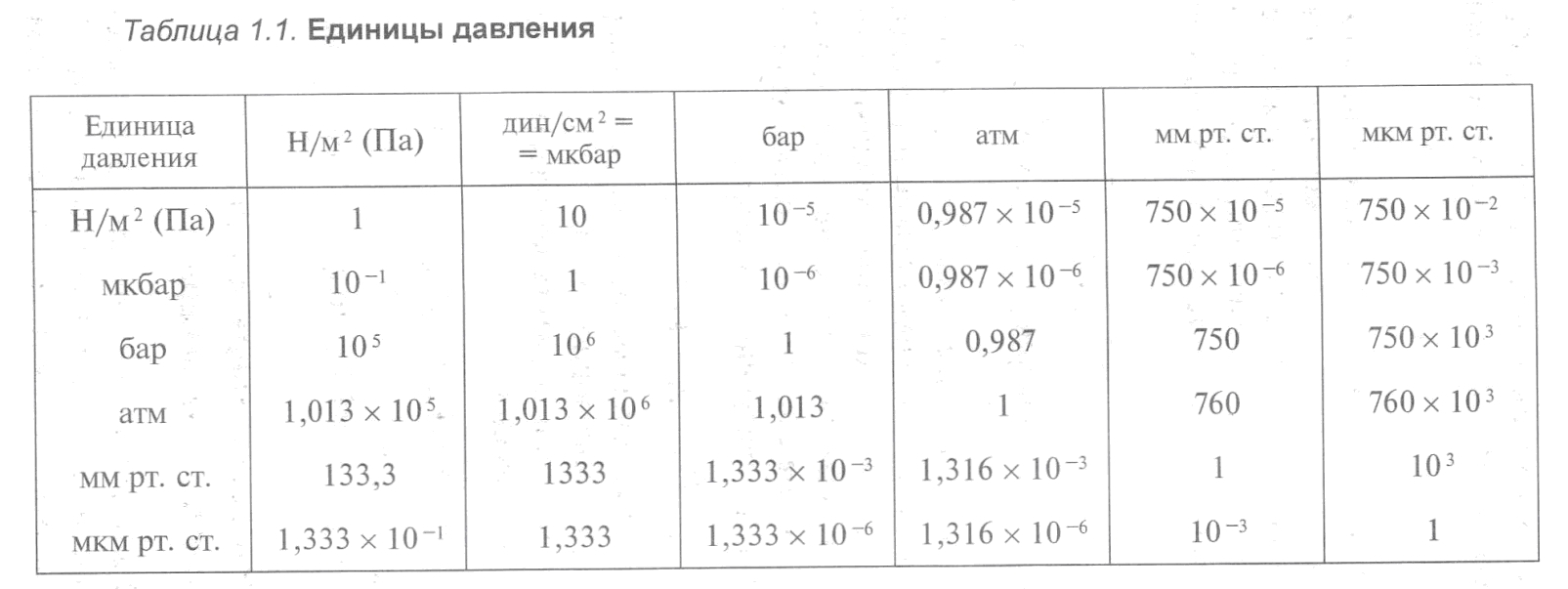
6. Единицей давления служит: в системе СИ — Н/м2 (ньютон на квадратный метр, или паскаль (Па)); в системе СГС — дин/см2 (дина на квадратный сантиметр, или микробар). Практической, внесистемной единицей давления газа является миллиметр ртутного столба (мм рт. ст.). В вакуумной технике единица давления газа «миллиметр ртутного столба» носит также название «Тор» (в честь итальянского физика Торричелли).
Между различными единицами давления имеются опре­деленные соотношения, которые полезно записать в виде табл. 1.1.
Уравнение состояния идеальных газов объединяет в себе газовые законы, известные из экспериментальной физики.
Закон Бойля—Мариотта. При постоянной массе Nm и тем­пературе произведение давления газа на его объем есть величина постоянная:

В более общем случае, когда постоянной остается только температура, а количество газа меняется, можно написать:

т. е. произведение давления газа на его объем при неизменной температуре прямо пропорционально массе газа. Отсюда следует, что величиной рV вполне определяется количество газа, если его температура остается неизменной.

 
При решении многих практических задач вакуумной техники бывает удобно количество газа выражать именно в единицах 
рV[(Н/м2) • м3 = Н • м, мм рт. ст. • см3] и т. п.
Из уравнений (1.4) и (1.1) следует, что

где р = Nm/V— плотность газа; таким образом, при постоянной температуре давление газа пропорционально его плотности.
Кроме понятия о плотности газа ρ как о массе в единице объема, полезно ввести понятие о молекулярной концентрации газа N₁ = N/V о количестве молекул в единице объема. Так как N₁m = ρ , то при постоянной температуре давление пропорционально также и молекулярной концентрации газа.
Закон Гей-Люссака. При постоянной массе Nm и давлении ρ объем газа пропорционален его абсолютной температуре:

Точно так же: при постоянной массе Nm и объеме V давление газа пропорционально его абсолютной температуре:

Соотношение (1.6) носит также название закона Шарля.
Закон Авогадро. При одинаковых давлениях и температурах в одинаковых объемах различных газов содержится одинаковое число молекул. Поскольку уравнение (1.2) справедливо для любого газа, решая его относительно N, получаем равенство

  (1.7)

непосредственно указывающее на справедливость закона Авогадро.
Закон Дальтона. Полное давление смеси химически не взаимодействующих газов равно сумме парциальных давлений отдельных газов. Парциальным давлением газа, входящего в смесь, называется то давление, которое этот газ имел бы, если бы в объеме смеси он был только один. Этот закон можно представить следующим образом:

где Рсм — полное давление смеси; р1 ,р2….., рп — парциальные давления газов, составляющих смесь.
Действительно, если выразить количества каждого газа в единицах рV, то, очевидно,

где Vсм — объем смеси.
После сокращения на Vсм получаем уравнение (1.8).