Вязкостный режим течения газа
2.3.2. Вязкостный режим течения газа
В вязкостных условиях сопротивление течению газа определяется его вязкостью. Молекулы газа, находящиеся вблизи стенок трубопровода, имеют меньшую скорость, чем молекулы, находящиеся вблизи оси (рис. 2.16). Составляющая ?x скорости молекул газа, прилегающих к стенке, в первом приближении равна нулю.
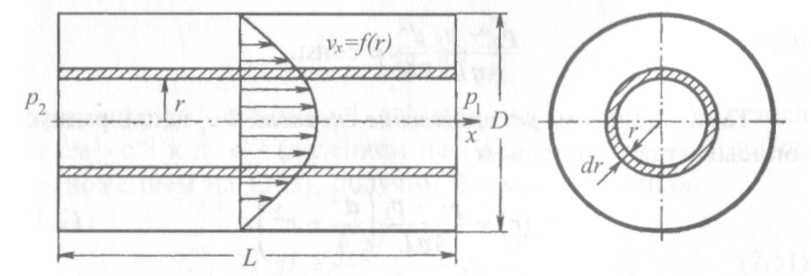
Рис. 2.16. Вязкое течение в цилиндрической трубе
Длинный трубопровод с круговым сечением
В канале с круговым сечением распределение скоростей имеет, очевидно, осевую симметрию. Столб газа, содержащийся в цилиндре радиусом r, перемещается под действием силы, равной произведению разности давлений р2 - р1 на поверхность ?r2:
А+ = ?r2 (р2 - р1). (2.39)
Эта сила уравновешивается силой трения А_, приложенной к цилиндрической поверхности 2 ?rL столба газа.
Учитывая коэффициент вязкости ? и обозначая через d?x/dr градиент составляющей скорости ?x по радиусу r, можно определить силу трения следующим образом:
A_ = -?2?rL (2.40)
Приравнивая силы А+ и А_, получим уравнение:
?r2(p2 - p1) = 2 ?rL? (2.41)
После интегрирования этого уравнения находим
(2.42)
После следующего интегрирования получаем
(2.43)
При r = d/2, т. е. на стенке, имеем ?x = 0 и, следовательно,
Таким образом, распределение скоростей ?x вдоль радиуса описывается уравнением
(2.44)
которое графически выражается параболой (см. рис. 2.16).
Элементарный объемный поток газа, проходящий со скоростью ?x кольцевую площадку радиусом r и шириной dr за период времени 1 с, выражается следующим образом:
(2.45)
где
p0=1/2(р2 + р1). (2.46)
есть среднее давление в потоке газа.
Вводя вместо ?x выражение (2.44), получаем
(2.47)
Объемный поток газа, проходящий в течение секунды через все сечение А канала (объемная скорость течения), будет равен
(р2 - р1) (2.48)
Таким образом, общий поток газа при давлении р0 определяется уравнением:
(р2 - р1) (2.49)
Отсюда можно определить проводимость канала для вязкостных условий:
(2.50)
(единицы: см3 · с-1, г · см-1 · с-1, дин · см2, см4, см). Переходя от см3 · с-1 к л · с-1 (делением на 1000) и от дин ·см2 к Тор (умножением на 1333), получим формулу Пуазейля:
(2.51)
Для воздуха при температуре окружающей среды (T ~ 293 К) коэффициент вязкости ?возд равен 1,8 · 10-4. Подставляя эту величину в формулу (2.51), получим:
(2.52)
(единицы: л · с-1, Тор, см4, см).
Из формулы (2.51) следует, что в вязкостных условиях проводимость цилиндрического канала прямо пропорциональна давлению и четвертой степени диаметра, а также обратно пропорциональна длине канала; кроме того, она зависит от рода газа и больше для газов с малой вязкостью, т. е. с малой молекулярной массой и большим размером молекул.
Короткие трубопроводы с некруговыми сечениями
Формулы для таких трубопроводов более сложны, и их часто получают эмпирическим путем. Различные формы сечения можно учесть, вводя коэффициент формы в формулы для трубопроводов кругового сечения.
Зависимость проводимости трубопровода в вязкостных условиях от рода газа
Проводимость трубопровода в вязкостных условиях для различных газов (по отношению к воздуху при Т = 293 К) можно представить зависимостью
(2.53)
где d0 — диаметр молекул, а М0 — молекулярная масса газа.
Молекулярно-вязкостный режим течения газа
Для промежуточных условий применяют эмпирические формулы, основанные на комбинации формул, полученных для молекулярных и вязкостных условий. Такой является формула Кнудсена:
![]()
где Uвязк — проводимость для вязкостных условий (2.51); UMOЛ — проводимость для молекулярных условий (2.26); а — коэффициент, который для воздуха (и подобных ему газов) при ~300 К описывается эмпирическим выражением:
![]()
где р0 измеряется в миллиметрах рт. ст., a d — в сантиметрах.
Коэффициент а в широком диапазоне давлений изменяется от 1,0 до 0,8. Принимая среднее значение а ~ 0,9, можно записать формулу (2.54) в простом виде:
![]()
Подставляя вместо UВЯЗК и UMOЛ соответствующие выражения, получим (для воздуха) формулу проводимости канала длиной L и диаметром d (при L » d) в широком диапазоне давлений:
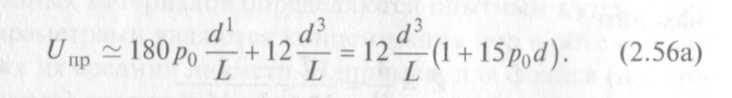
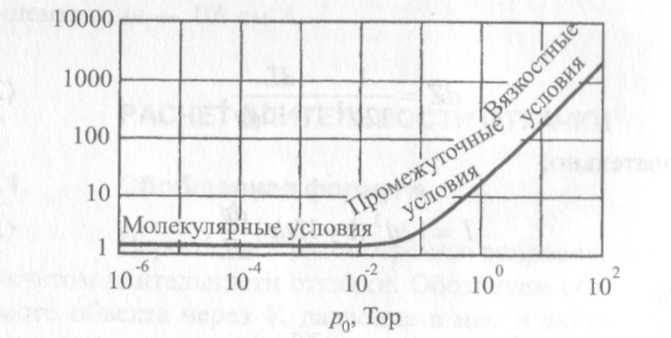
График, показанный на рис. 2.17, представляет собой зависимость проводимости для воздухопровода (длиной L = 10 см и диаметром d = 1 см) от давления р0.
