Течение газа
Стационарный газовый поток через элементы вакуумной системы является следствием существующей в них разности давлений, и рассчитывается по формуле
где р1 и р2 — давление на концах элемента вакуумной системы, а U — проводимость этого элемента. Проводимость элемента является коэффициентом пропорциональности между потоком и разностью давления и численно равна количеству газа, протекающему через элемент в единицу времени, при разности давлений на концах элемента, равной единице. Если выразить поток в единицах л·торр/с или м3·Па/с, то проводимость выразится соответственно в л/с и м3/с. Выражение потока в кг/с даёт для проводимости размерность кг/(Па·с).
Сопротивление элемента — это величина, обратная его проводимости
По аналогии с электрическими цепями в вакуумной технике при приближённом рассмотрении процессов течения газа принимается, что проводимость элемента не зависит от его расположения среди других элементов. Тогда для ряда i параллельно соединённых элементов с проводимостями Ui можно определить общую проводимость как
где N – общее число элементов.
Для ряда последовательно соединённых элементов получим общую проводимость:
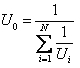 . (1.49)
. (1.49)Проводимость элемента вакуумной системы зависит от степени вакуума, при котором наблюдается течение газа. В низком вакууме проводимость растёт при повышении давления. В высоком вакууме она остаётся постоянной.
В низком вакууме основную роль играет вязкостный режим течения газа, при котором характер распределения скорости в поперечном сечении определяется силами внутреннего трения.
При высоком вакууме силы внутреннего трения в газах стремятся к нулю, и существует молекулярный режим течения газа, для которого характерно независимое перемещение отдельных молекул. В среднем вакууме на течение газа одновременно сказывается влияние внутреннего трения и молекулярного переноса. Существующий при этом режим течения называют молекулярно-вязкостным.
В качестве примеров рассмотрим течение газа для двух типов элементов вакуумных систем: отверстий и трубопроводов.
Под отверстием понимается трубопровод, длина которого значительно меньше диаметра, расположенный в стенке и разделяющий два объёма с давлениями р1 и р2 соответственно.
При вязкостном режиме течения газа закон сохранения энергии для адиабатического истечения газа можно записать в виде равенства приращения кинетической энергии газа изменению его энтальпии
где G — поток газа; ![]() — скорость газа на выходе из отверстия; I1 и I2 — энтальпии газа до и после прохождения отверстия. Воспользовавшись тем, что I = срТ перепишем уравнение сохранение энергии в виде
— скорость газа на выходе из отверстия; I1 и I2 — энтальпии газа до и после прохождения отверстия. Воспользовавшись тем, что I = срТ перепишем уравнение сохранение энергии в виде
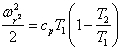 . (1.51)
. (1.51)С учётом того, что рV = RT/M, R/M = cp – сν ; γ= cp/сν; V1/V2 = (p2/p1)1/V, где V — удельный объём газа, м3/кг, преобразуем (1.51):
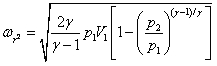 . (1.52)
. (1.52)Поток газа через отверстие (кг/с) с учётом записанного выражения для :
где ![]() ; r = p2/p1, А — площадь отверстия.
; r = p2/p1, А — площадь отверстия.
Из уравнения газового состояния следует, что
Тогда (1.53) можно переписать в виде
В условных единицах массы Па·м3/с выражение для газового потока (1.55) будет иметь следующий вид:
При вязкостном режиме течения газа уменьшение отношения давления с обеих сторон отверстия r = р2/ p1 ≤ 1 приводит к тому, что количество газа, протекающего через диафрагму, и конечная скорость потока в области р2 увеличиваются до тех пор, пока отношение р2/ p1 не достигнет критического значения, соответствующего скорости звука. Если процесс истечения адиабатический, то критическое значение:
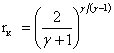 . (1.57)
. (1.57)Для воздуха γ = 1,4, поэтому rк = 0,528; для одноатомного газа γ = 1,67; rк = 0,437, для трёхатомного газа γ = 1,4; rк = 0,546.
Дальнейшее уменьшение отношения давления не изменяет количества протекающего газа. В области отношений р2/ p1 выше критического проводимость определяется выражением
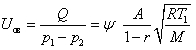 . (1.58)
. (1.58)Для воздуха и других двухатомных газов при γ = 1,4 получим
где М — молекулярная масса, кг/кмоль; А — площадь отверстия, м2 ; Uов выражено в м3/с.
При комнатной температуре для воздуха (М = 29 кг/кмоль), если А выражено в м2, получим для проводимости отверстия
(1.60)
Так как отношение давлений r заранее неизвестно, то расчет нужно вести методом последовательных приближений. При проектировочном расчете с большим запасом можно принять в первом приближении, что Uов = 200 А, м3/с и не зависит от r. Тогда для круглых отверстий Uов=160d2 м3/с. Если dвыражено в см, то Uов=160d2 , л/с. В обычных вакуумных системах, работающих в стационарном режиме чаще всего r ≥ 0,8, это соответствует проводимости Uов = 830 А, м3/с, что примерно в 4 раза выше, чем первое приближение.
Проводимость отверстия в молекулярном режиме рассчитывается по формуле
где G = G1– G2; G1 и G2 — массовые потоки через отверстие, проходящие навстречу друг другу. С учётом того, что G1 = n1mυ ар1А/4, а G2 = n2mυ ар2А/4, для проводимости можно записать при Т = const
где М в кг/моль, Т в К, А в м2, Uом в м3/с.
Расчёт проводимости отверстия для воздуха (М = 29 кг/кмоль) при комнатной температуре Т = 298 К из (1.62) даёт в результате
Так как для круглого отверстия А = πd2/4, то Uом = 91 d2 м3/с; если d выражено в см, то Uом = 91 d2 л/с.
В области молекулярно-вязкостного режима течения можно пользоваться приближённой формулой:
где 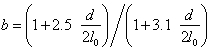 , которая справедлива также в областях молекулярного и вязкостного режимов течения газа.
, которая справедлива также в областях молекулярного и вязкостного режимов течения газа.
Для воздуха при комнатной температуре имеем
причём коэффициент b на границе с вязкостным режимом равен 0,8, а на границе с молекулярным – 1,0. Для приближённых расчётов можно принять b = 0,9.
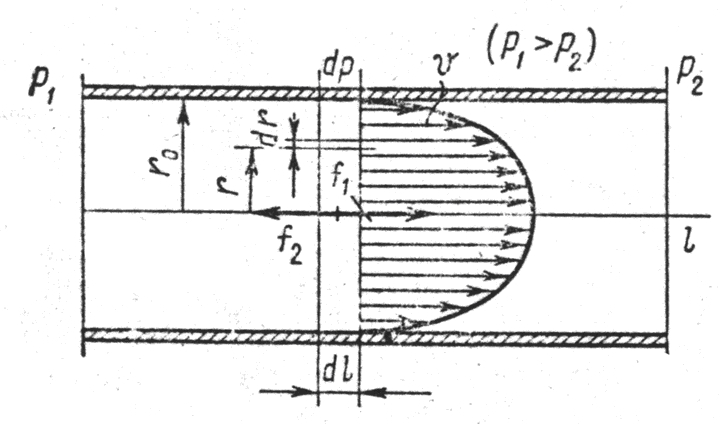
В области низкого вакуума при вязкостном режиме течения газа средняя длина свободного пути молекул газа l0 значительно меньше диаметра трубопровода. Слой газа у поверхности трубопровода остаётся неподвижным, а остальные слои толщиной l0 движутся в условиях стационарного потока с постоянной скоростью. Ограничимся рассмотрением трубопровода с круглым поперечным сечением.
При стационарном потоке в малом элементе газового цилиндра, образованного на радиусе r приращением dr (рис. 1.6а), существует равновесие движущей силы f1 = πr2dp, вызываемой разностью давлений, и силы внутреннего трения в газах ![]() .
.
Условие равновесия можно записать в виде
Принимая dυ/dr, не зависящим от l ( распределение скоростей по всей длине трубопровода постоянно), после интегрирования в пределах от 0 до lполучим
Вновь интегрируя по радиусу трубопровода, при начальных условиях r = r0 , υ = 0 получим параболическое распределение скоростей по сечению трубопровода:
Объёмный расход газа
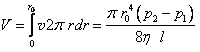 . (1.69)
. (1.69)Поток газа Q, протекающий через трубопровод, найдём как произведение объёмного расхода V на среднее давление в трубопроводе:
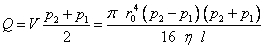 . (1.70)
. (1.70)
 |
 |
| а) | б) |
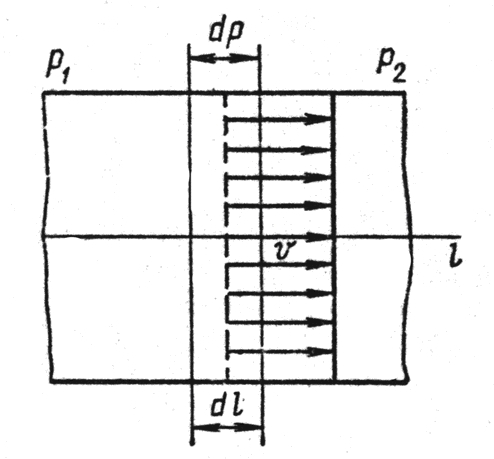
Рис. 1.6. Схема течения газа в трубопроводе:
а) при вязкостном режиме; б) при молекулярном режиме
Запишем выражение для проводимости при вязкостном режиме течения:
Таким образом, проводимость круглого трубопровода при вязкостном режиме течения газа обратно пропорциональна его длине и коэффициенту динамической вязкости газа, прямо пропорциональна среднему давлению в трубопроводе и четвёртой степени радиуса трубопровода.
Для воздуха при Т = 293 К:
можно преобразовать к виду
Здесь d и l — в м; p — в Па; а Uтв — в м3/с. Это же выражение, если d и l — в см; p — в торр, а Uтв — в л/с, имеет вид
При высоком вакууме и молекулярном режиме течения газа длина свободного пути молекул газа больше диаметра трубы, молекулы движутся независимо друг от друга, соударяясь лишь со стенками трубопровода. Будем считать, что каждая из молекул, хаотически движущихся в трубопроводе, имеет постоянную составляющую переносной скорости υ п, направленной по оси трубопровода в область с меньшим давлением.
Движущая сила в этом случае
где А — поперечное сечение трубопровода.
Уравновешивающая сила, равная общему изменению количества движения всех молекул при их ударе о стенку трубки:
где В — периметр трубопровода; 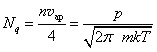 – число молекул, ударяющихся о единицу поверхности в единицу времени.
– число молекул, ударяющихся о единицу поверхности в единицу времени.
Уравнение равновесия f1 + f2= 0 можно записать, в виде
Если в (1.76) ввести объемный расход V = υ пA и подставить выражение для Nq , то получим
В стационарном режиме произведение pcp = Q = const , где pср= (p1 + p2)/2 . Проинтегрируем это отношение в пределах от p1 доp2:
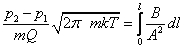 . (1.79)
. (1.79)Откуда поток газа
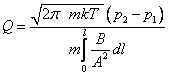 , (1.80)
, (1.80)для υap, имеем
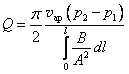 . (1.81)
. (1.81)Более точное выражение для Q получено Кнудсеном с учетом функции распределения молекул по скоростям:
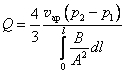 . (1.82)
. (1.82)Проводимость трубопровода в этом случае
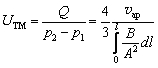 . (1.83)
. (1.83)Для трубопровода постоянного поперечного сечения имеем
В случае круглого поперечного сечения
где d и l выражено в м; М — в кг/кмоль; Т — в К; U — в м3/с. Таким образом, проводимость трубопровода при молекулярном режиме течения не зависит от давления.
Для воздуха при 293 К проводимость цилиндрического трубопровода круглого поперечного сечения
Если выражать d и l в см, а U — в л/с, то формула для расчёта проводимости (1.50) примет другой вид:
Повышение давления в закрытом вакуумном сосуде с течением времени указывает на наличие негерметичности (течи).
Действительная негерметичность возникает вследствие неточности соединений, образования трещин, несовершенства в изготовлении или вследствие применения материала, проницаемого для газов.
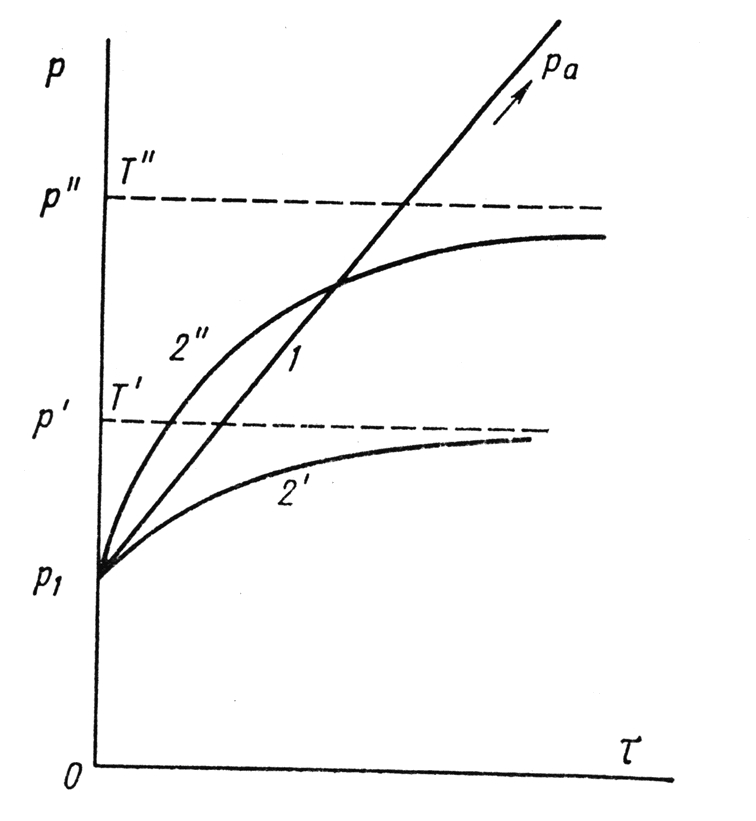
Рис. 1.7. Рост давления р со временем τ при действительной и мнимой негерметичности:
l — действительная негерметичность, давление растёт вплоть до атмосферного; 2 — мнимая негерметичность, давление устанавливается на определённом уровне p' (при T') или p"(при T")
Мнимая негерметичность проявляется как десорбция газов с поверхностей, находящихся в вакуумном пространстве, а именно со стенок, электродов и т.д. : обычно она связана с применением неподходящих материалов и недостаточным обезгаживанием вакуумной системы.
Действительной негерметичности соответствует в целом линейное возрастание давления в системе со временем (рис. 1.7), ибо поток газа из окружающей среды в вакуумную систему (при низком давлении р в ней). В самом деле, поток газа через действительную негерметичность
можно считать постоянной величиной. В формуле (1.88) величина ра (ра>> р) обозначает атмосферное давление.
В случае мнимой негерметичности по мере возрастания давления в системе десорбция уменьшается и становится равной нулю в момент установления состояния равновесия при определённых давлении р1 и температуре Т1. При более высокой температуре Т2 равновесное давление р2 будет также выше.
