Отверстие в бесконечно тонкой пластине можно рассматривать как своего рода канал, соединяющий два про­странства, разделенные этой плоскостью. Такое отверстие можно считать объемом бесконечно малой длины с попереч­ным сечением А0.
Проводимость U0 отверстия определяется формулой (2.6), из которой следует, что проводимость эквивалентна объемной скорости течения S0 газа, втекающего под давлением р в отвер­стие, когда давление с другой стороны отверстия равно нулю.
Если за отверстием начинает­ся трубопровод (длиной L и сече­нием А0), в который поступает газ (рис. 2.4), то поток газа в плоско­сти отверстия при давлении р1 ока­жется меньшим по сравнению со случаем, когда трубопровод за от­верстием отсутствует (т. е. его дли­на равна нулю). Это связано с тре­нием газа о стенки трубы.

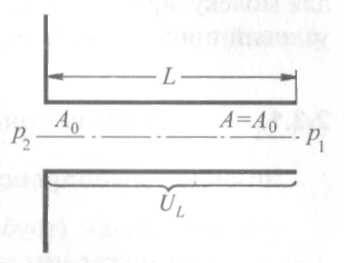
Рис. 2.4. Проводимость тру­бопровода с поперечным се­чением А и длиной L

Влияние трения в вязкостных условиях понятно, в молекулярных же условиях, когда определяющими становятся столкнове­ния молекул со стенками, явление трения можно истолко­вать следующим образом.

Небольшая часть молекул газа, попадающих на вход тру­бопровода L , поступает непосредственно в отверстие А0, ос­тальные же ударяются о стенки трубопровода. Эти молекулы не сразу отражаются от стенок, а некоторое время удержива­ются на поверхности (межмолекулярными силами). Направ­ления их последующего вылета с поверхности стенок описы­ваются рассмотренным выше вероятностным распределением (закон Кнудсена). В связи с этим часть составляющей скорости молекул в направлении движения теряется. Чем длиннее тру­бопровод и чем меньше его диаметр, тем больше таких отраже­ний и, следовательно, больше сопротивление течению газа.
Таким образом, импеданс отверстия Z0 = 1/U0 возрастает на величину Z = 1/UL, и импеданс трубопровода вакуумной системы выражается формулой:

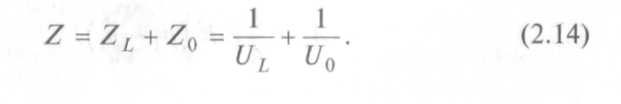
Когда длина трубопровода L уменьшается до нуля, импе­данс ZL становится равным нулю, а импеданс отверстия Z0 остается неизменным. Импеданс отверстия можно не учиты­вать лишь в тех случаях, когда длина трубопровода намного больше его диаметра.
Теория позволяет вычислить проводимость трубопровода для молекулярных и вязкостных условий; для промежуточных условий проводимость определяется путем интерполяции.

2.3.1.  Молекулярный режим течения газа

 

Длинный трубопровод с круглым сечением

Обычно каналы (трубопроводы) имеют конечную длину, а их сечение может иметь различные формы. Наиболее про­стым трубопроводом является цилиндрическая труба круго­вого сечения диаметром d и длиной L, на одном конце кото­рой давление равно p1 на другом — р2(р2> р1) Предполага­ется, что L » d (рис. 2.5).

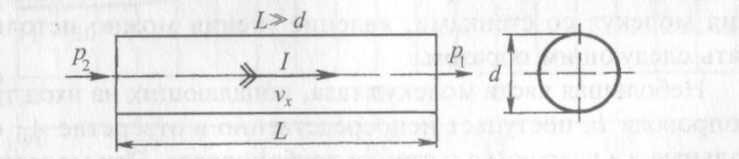
Рис. 2.5. Цилиндрический трубопровод длиной L и диаметром d

В случае  d молекулы газа движутся индивидуально; часть их движется непосредственно по трубе, не касаясь сте­нок, другие же соударяются со стенками и перемещаются зиг­загообразно. Ввиду того что период пребывания на стенке име­ет конечную величину, молекула теряет часть скорости в на­правлении оси канала х, что равнозначно трению газа о стенки.
Так как сила трения преодолевается перепадом давлений р2 — p1 то должно выполняться условие равновесия двух сил:
1) силы А+, соответствующей перепаду давлений р2 — р1 и действующей на «столб» газа с основанием 1/4?d2,

2) силы трения А_, определяемой частотой соударений ?'?dL молекул газа со стенками трубы (площадью ?dL) и составляющей ?x скорости массы газа.
Частота соударений в 1 с определяется формулой ?'?dL=1/4 n0?a?dL  (2.16)

где n0 — средняя концентрация, вычисляемая по среднему давлению

p0=1/2(p1+p2) (2.17)

как 
n0=p0 /kT (2.18)

Что касается составляющей скорости ?x, то ее находят, принимая во внимание то, что изменение количества движе­ния молекулы при соударении со стенкой равно m0?x.
Произведение частоты соударений ?'?dL на изменение количества движения m0?x дает полное изменение количе­ства движения в секунду, или силу трения:

A_= ?'?dLm0?x =1/4 n0?a?dLm0?x    (2.19)

Из равенства A+ = A_ следует

1/4?d2(p1+p2) = 1/4 ?dLn0m0?а?x          (2.20)

Отсюда после подстановки p0 вместо n0 находим

 

Движение столба газа с основанием 1 /4d2 со скоростью x эквивалентно объемной скорости течения 1/4?d2x , т. е.

Учитывая давление р0, получаем общий поток газа

Из более строгого рассмотрения с учетом отношения ско­ростей x / a и удаления различных точек течения от стенок трубы следует, что выражение (2.23) должно содержать мно­житель 8/3 (~0,85); таким образом,

Подставляя в формулу (2.23) вместо x выражение (2.21), а в нем вместо ?a –выражение

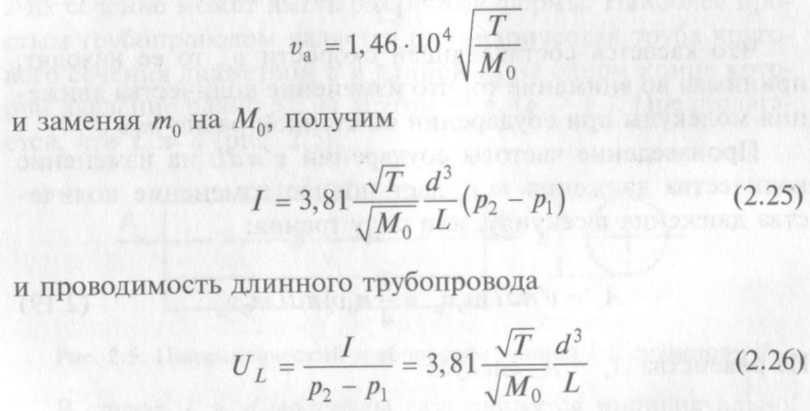
(единицы: л · с-1, К, г · моль-1, см3, см).
Проводимость трубопровода прямо пропорциональна его диаметру в третьей степени и обратно пропорциональна длине, она возрастает с повышением температуры и с уменьшением молекулярной массы газа.
При Т= 293 К и М0 = 29 (например, для воздуха) прово­димость длинного трубопровода

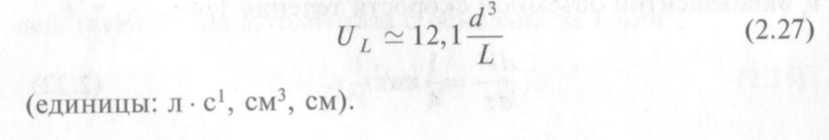
Другой вид формулы для проводимости трубопровода (в от­ношении воздуха). Заменяя в формуле (2.27) диаметр d радиу­сом r = 1/2dи выражая его в миллиметрах, длину L — дли­ной l (также в миллиметрах), получаем формулу (для возду­ха) в более легком для запоминания виде:

 

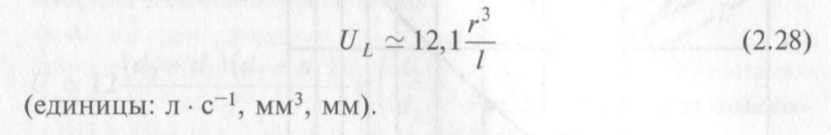
Трубопроводы с не круговым сечением

Во многих случаях проводимость трубопроводов с не кру­говыми сечениями можно вычислить, заменяя не круговое сечение круговым с такой же площадью. В особых случаях применяют специальные формулы.
Длинный трубопровод с прямоугольным сечением. Проводи­мость трубопровода длиной L с прямоугольным сечением ши­риной а и высотой b (L » а ~ b) для воздуха при комнатной температуре описывается формулой:

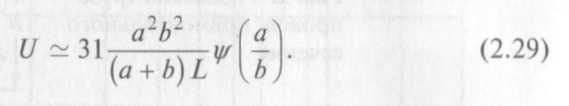
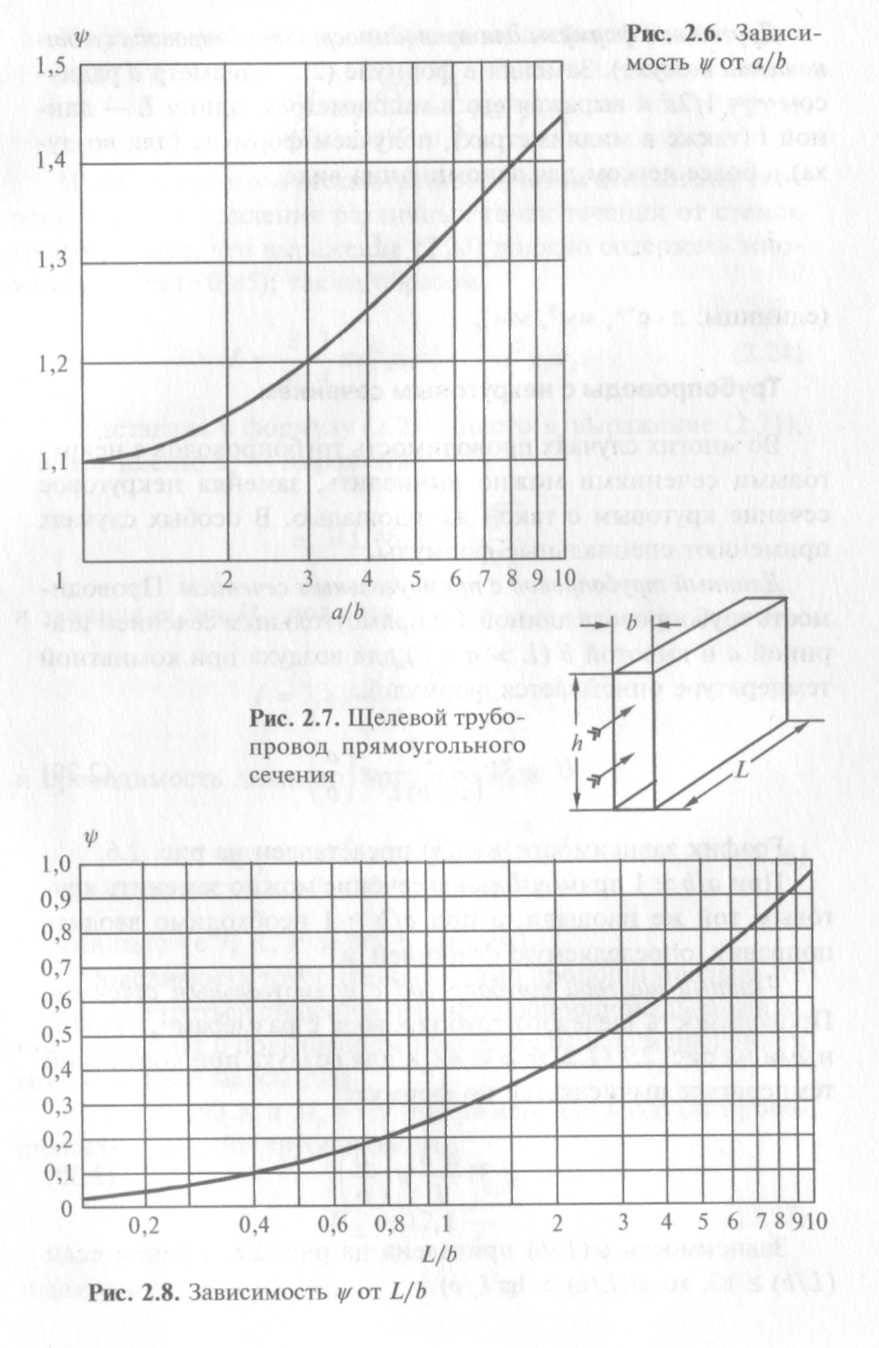
График зависимости ?(а/b) представлен на рис. 2.6.
При а/b ~ 1 прямоугольное сечение можно заменить кру­говым той же площади, а при а/b > 1 необходимо вводить поправку, определяемую функцией ?.
Длинный щелевой трубопровод с прямоугольным сечением. Проводимость щелевого трубопровода с размерами, указан­ными на рис. 2.7 (L » h,b«h?0), для воздуха при комнатной температуре вычисляется по формуле:

Зависимость (L/b) приведена на рис. 2.8, причем если (L/b) ?10, то ?(L/b) ~ lg(L/b).

Длинный трубопровод с коль­цевым сечением. Проводимость длинного трубопровода с коль­цевым сечением (рис. 2.9) для воздуха при комнатной темпера­туре вычисляется по формуле

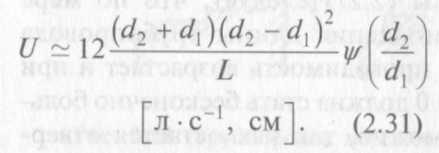
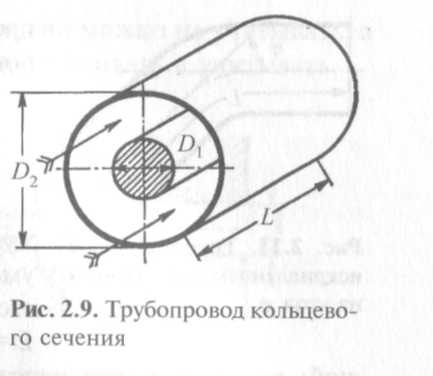
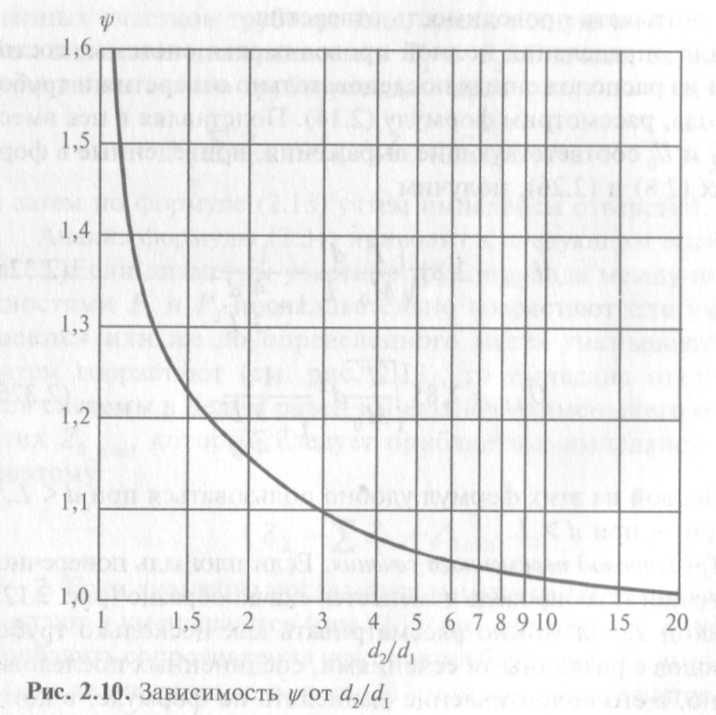
Зависимость ? (d2/d1) для такого трубопровода представ­лена на рис. 2.10.

Искривленный трубопровод. Изгиб или излом трубопрово­да на угол ? (рис. 2.11) приводит к некоторому изменению проводимости, которое можно учесть поправкой на длину канала L:

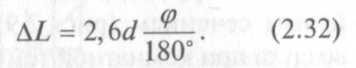
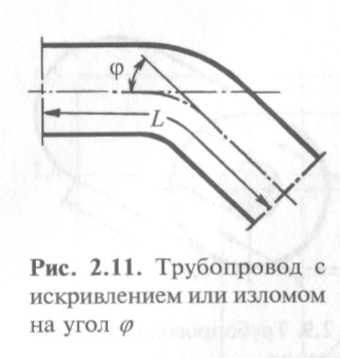
Короткие трубопроводы. Из фор­мулы (2.27) следует, что по мере уменьшения длины трубопровода его проводимость возрастает и при L = 0 должна стать бесконечно большой; разумеется, это невозможно, так как остается отвер­стие, проводимость которого конечна.
Таким образом, формула (2.27) справедлива только для длинных трубопроводов, для коротких же трубопроводов сле­дует учитывать проводимость отверстия.
Для определения полной проводимости системы, состо­ящей из расположенных последовательно отверстия и трубо­провода, рассмотрим формулу (2.14). Подставляя в нее вмес­то UL и U0 соответствующие выражения, приведенные в фор­мулах (2.8) и (2.26), получим:

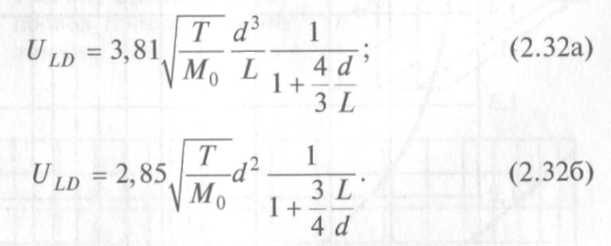
Первой из этих формул удобно пользоваться при d < L, а второй — при d > L.
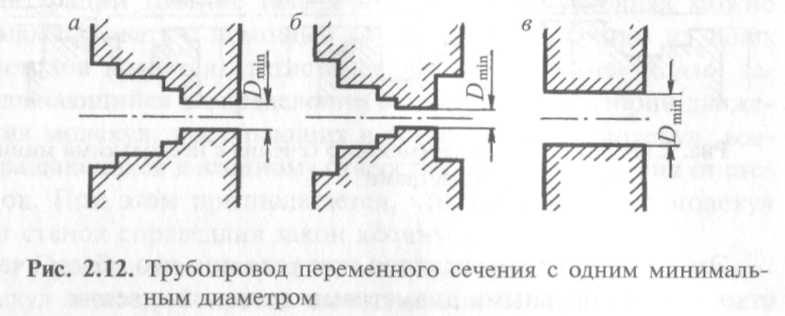
Трубопровод переменного сечения. Если площадь поперечно­го сечения трубопровода изменяется скачкообразно (рис. 2.12), то такой канал можно рассматривать как несколько трубо­проводов с различными сечениями, соединенных последова­тельно, а его сопротивление вычислять по формуле, в кото­рой Z1 Z2, ... являются импедансами отдельных участков:
Z= Z1 +Z2 + Z3 +....   (2.33)

При Ln » dn импедансы отверстий можно не учитывать, а при Ln « dn необходимо их точно оценивать и учитывать

Рассмотрим для примера систему последовательно соеди­ненных участков трубопровода, заключенную между двумя бесконечными поверхностями Р1 и Р2. Сначала определим импедансы самого трубопровода в виде
? ZL = ZL1+ZL2+ ZL3+... ,                                                       (2.34)
а затем по формуле (2.13) учтем импедансы отверстий.
Анализ формулы (2.34) приводит к следующим выводам.
1. Если диаметры участков трубопровода между поверхностями Р1 и Р2 последовательно возрастают или уменьшаются или же до определенного места уменьшаются, а затем возрастают (см. рис. 2.12), то импеданс отверстия для системы в целом равен импедансу наименьшего отверстия Z0 min, который следует прибавить к импедансу ZL, а поэтому
Z? = ?ZL+Z0min.                                 (2.35)
2. Если диаметры последовательных участков канала возрастают и уменьшаются (рис. 2.13), то к импедансу ZL нужно прибавить сопротивления участков трубопровода с минимальными диаметрами, т.е. полный импеданс определяется следующим образом:
Z? = ?ZL+?Z0min.                                      (2.36)

 

Это уравнение справедливо при условии, что объем уча­стков с минимальными диаметрами достаточно велик
Вышеприведенные соображения относятся также к тру­бопроводам с диафрагмами d1/2 и d2/3 (рис. 2.14). Импеданс вакуумной системы, представленной на рис. 2.14, описыва­ется приближенной формулой

 

(2.37)

где Zl/2, Z2/3 — импедансы отверстий с диафрагмами

Конический трубопровод. Для трубопровода в виде усечен­ного конуса (рис. 2.15) эквивалентный диаметр вычисляется по формуле: (2.38)

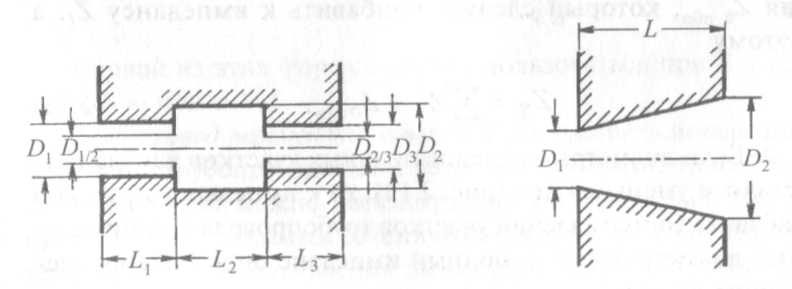
                 Рис. 2.14. Трубопроводы с диафрагмами Рис. 2.15. Конусообразный трубопровод

 

Другие методы вычисления проводимости

В случае систем или трубопроводов более сложной кон­фигурации течение газа в молекулярных условиях можно анализировать с помощью других методов. Одним из таких методов является статистический метод Монте-Карло, за­ключающийся в определении возможных траекторий движе­ния молекул, поступающих в трубопровод, и молекул, воз­вращающихся к входному отверстию после отражения от сте­нок. При этом предполагается, что для отражения молекул от стенок справедлив закон косинуса.
При большом количестве молекул вероятности прохода мо­лекул через трубопровод вычисляют на ЭВМ, а проводимость входного отверстия умножают на этот показатель. Можно при этом дополнительно учитывать характеристики поверхностей (стенок), с которыми сталкиваются молекулы, и потерю скорос­ти молекул (коэффициент прилипания и время пребывания).
Метод Монте-Карло трудоемок, особенно в применении к вакуумным системам сложной конфигурации. Упрощен­ным вариантом его является метод графоаналитического мо­делирования на плоскости.