Самым простым элементом вакуумной системы, на котором может возникнуть перепад давлений (р2 — р^, является отверстие (рис. 2.1). 
Предполагается, что отверстие, имеющее площадь А0, сделано в плоскости бесконечно тонкой и неограниченной по ве­личине пластины, т. е. молекулы попадают в отверстие из объема 2 под пространственным углом 180° и под таким же углом выходят в объем 1, причем во всех точках объемов 1 и 2 господствуют давления со­ответственно pi и р2. Если р2 > pv то газ течет из объема 2 в объем 1.

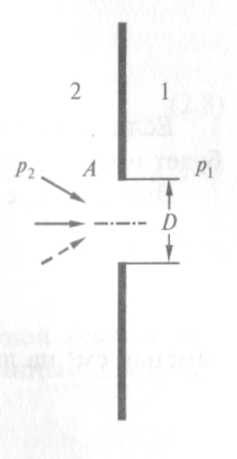
Рис. 2.1. Проводимость отверстия площадью А (ди­аметром D) в плоской стенке неограниченных раз­меров (1,2 — области вакуумной системы)

2.2.1.  Молекулярный режим течения газа

В случае молекулярных условий (? » d) вывод выражения для проводимости отверстия довольно прост. Количества молекул газа, проходящих за 1 с через 1 см2 площади отверстия со стороны а и со стороны b, соответственно равны.

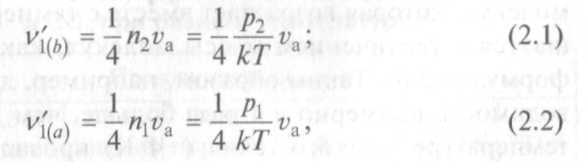
а количество молекул, прошедших за 1 с в направлении от а к b, описывается формулой

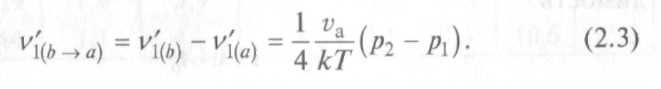
Поток газа через отверстие площадью А0 согласно фор­муле (2.3) составит:

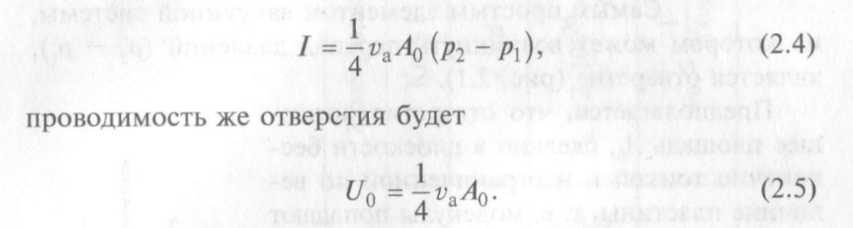
Если скорость ?a выражена в см · с-1, А0 — в см2, то U будет иметь размерность см3·с-1. 
Выражая ?a с помощью формулы

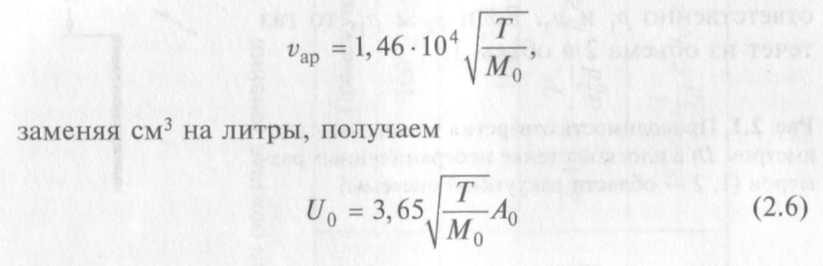
(единицы: л · с-1, К, г-моль-1, см2).
Следовательно, проводимость отверстия пропорциональна его площади. Форма отверстия не оказывает существенного влияния на его проводимость, за исключением случая щели, длина которой соизмерима с ?.
Из формулы (2.5) видно, что коэффициентом пропор­циональности является средняя арифметическая скорость молекул, которая возрастает вместе с температурой и умень­шается с увеличением массы молекул, как это вытекает из формулы (2.6). Таким образом, например, для водорода про­водимость примерно в 4 раза больше, чем для воздуха. При температуре жидкого гелия (~4 К) проводимость в ~9 раз меньше, чем при комнатной температуре (~300 К). Для воз­духа при комнатной температуре (М0 = 29, Т= 293 К) прово­димость
U0 ~11,64A0                                                                                                   

(единицы: л · с 1, см2), а удельная проводимость для воз­духа
U01 =11,6 л · с-1 · см-2.                                                                  

В случае круглого отверстия диаметром D0 имеем

что после подстановки в формулу (2.6) дает

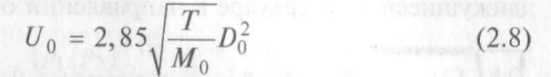
(единицы: л · с-1, К, г-моль-1, см2). для воз­духа Т= 293 К
U0 =9,1.                                                                                     (2.9) 
(единицы: л · с-1, см).
Проводимость для газа X с молекулярной массой М0,Х при температуре Т находят по известным данным для возду­ха из формулы:

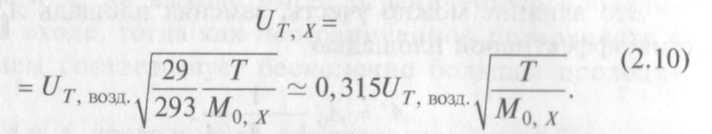
В табл. 2.2 приведены значения удельной проводимости круглого отверстия U01 для водорода, воздуха и углекислого газа при некоторых характерных температурах.

Таблица 2.2. Удельная проводимость отверстия в молекулярных условиях для Н2, воздуха и С02 при разных температурах

Отверстие в стенке конечных размеров

Если поверхность, в которой имеется отверстие, не беско­нечна, а имеет ограниченную площадь А (рис. 2.2), то проводи­мость отверстия А0 увеличивается по мере уменьшения отно­шения А/А0. В случае цилиндрического резервуара с отверсти­ем в основании цилиндра увеличение проводимости отверстия вызывается в некоторой степени фокусирующим действием, которое оказывает цилиндр диаметром D на молекулы газа, движущиеся в резервуаре в направлении отверстия А0.

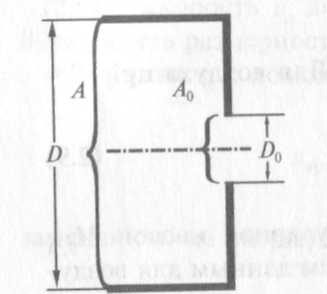
Рис. 2.2. Проводимость отверстия площа­дью А0 (диаметром D) в стенке конечных размеров (площадью А и диаметром D)

Это влияние можно учесть, заменяя площадь А0 отвер­стия эффективной площадью:
(2.11)
При А = А0 резервуар превращается в трубопровод с по­перечным сечением, равным площади отверстия.
Вводя в формулу (2.11) А' вместо А0, получим следующее выражение для проводимости отверстия (в случае воздуха):
(2.12)
Полное сопротивление отверстия в стенке конечных раз­меров определяется формулой:
(2.13)
где U0 и U — проводимости отверстий диаметром D0 и D соответственно/

2.2.2. Вязкостный режим течения газа

Формулы, описывающие течение газа в вязких условиях через отверстия, значительно сложнее, а проводи­мость зависит от отношения давлений р2/р1 перед отверсти­ем и после него.
Например, удельная проводимость отверстия для возду­ха при Т ~ 300 К и р2 ~ 760 Тор вычисляется по формуле Прандтля:

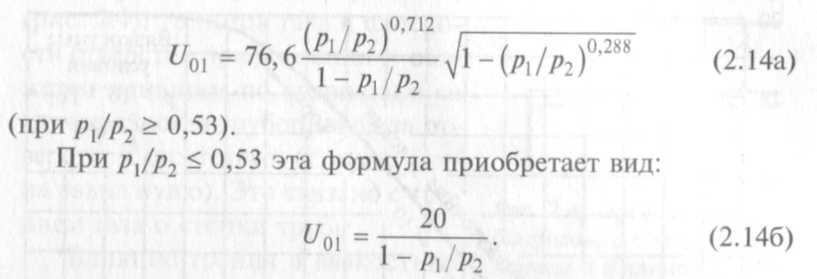
Следует учесть, однако, что цилиндр диаметром D с отверстием А0 на выходе имеет ограниченную проводи­мость на входе, тогда как неограниченной поверхности с отверстием соответствует бесконечно большая проводи­мость.
При А = А0 проводимость отверстия становится бесконеч­но большой, так как оно составляет бесконечно малую часть трубопровода, имеющего конечную проводимость. А при p1/p2 « 0,53.
U01 ~ 20 л · с1 · см                                                                          (2.14в)
Как следует из формулы (2.14в), при малых давлениях p1, в вязкостных условиях проводимость не зависит от p1.

2.2.3. Молекулярно-вязкостный режим течения газа

Еще более сложными становятся рассмотренные выше зависимости для промежуточных условий.
На рис. 2.3 показана в качестве примера зависимость удельной (на 1 см2) проводимости отверстия U01 для воздуха при температуре 293 К от числа Кнудсена d/?, с помощью которого давление р0 выражается как р0 = (d/?0) · 10-3 (для отверстия d = 5 см). Как видно из кривой, при р < 10-4 Тор имеет место явно выраженный молекулярный режим те­чения U01 ~ 12 л · с-1 · см-2, при р > 1 Тор - вязкостный U01 ~ 20 л · с-1 · см-2, а при 10-3 ? р ? 10-1 Тор - промежу­точный.

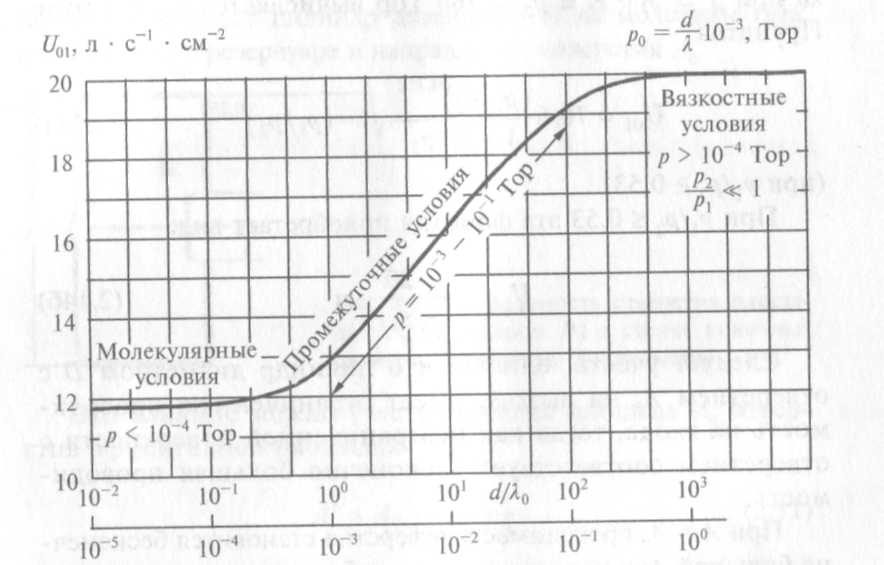
Рис. 2.3. Зависимость удельной проводимости отверстия U01 (диа­метром d = 5 см) от числа Кнудсена d/?0 для воздуха при температуре 293 К