Длина свободного пробега

Рассмотрим монохроматический пучок частиц со скоростью υ . Пусть пучок влетает в среду с постоянной концентрацией молекул n. Частицы пучка могут испытывать столкновение с молекулами, при этом будем считать их выбывшими из пучка. Обозначим направление вдоль пучка через l. Пусть < l > — средняя длина свободного пробега между столкновениями, тогда вероятность столкновения одиночной частицы входного пучка при прохождении расстояния dl определяется выражением dl /< l >. Изменение числа частиц dN в пучке при прохождении слоя от l до l + dl определяется выражением

,                              (1.26)

где N(l) — число частиц, приходящих в сечение l. Решая это дифференциальное уравнение, получим

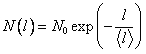,                         (1.27)

где N₀ — начальное число частиц в пучке.
Нормируя на начальное число частиц в пучке, можно получить выражение для плотности вероятности распределения частиц по длине свободного пробега

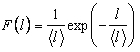.                         (1.28)

Тогда вероятность события, состоящего в том, что длина свободного пробега частицы не превышает L, определяется выражением

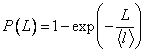.                         (1.29)

Для того чтобы выяснить, от чего зависит длина свободного пробега, рассмотрим модель абсолютно жестких шариков. Будем считать, что влетающие в среду частицы представляют собой жесткие шарики диаметром D, а молекулы среды имеют бесконечно малый размер. В рамках рассматриваемой модели будем называть сечением частицы ее поперечное сечение σ =π D² /4. Учет конечного размера молекул среды D₀ приводит к выражению для сечения σ = π(D+D₀) ² /4, а при D₀ = D получим соответственно:

Если принять за диаметр D размер первой боровской орбиты 2a₀ ~ 1 Å, то σ ~ 3.1×10^–16 см2. Величина πa₀² определяет характерный порядок атомных сечений и часто используется в качестве единицы измерения атомных сечений.
За время t частица входного потока проходит расстояние l = υ t, и покрывает объем σl. Среднее число молекул среды в этом объеме или, что то же самое, среднее число столкновений υ = nσl. Среднюю длину свободного пробега определим как расстояние < l >, при прохождении которого частица сталкивается в среднем с одной молекулой среды, то есть

.                                   (1.31)

Если скорость частицы υ постоянна, то среднее время свободного пробега

.                                  (1.32)

Воспользовавшись уравнением (1.24), можно представить среднюю длину свободного пробега в виде

,                                  (1.33)

то есть, при постоянной температуре средняя длина свободного пробега обратно пропорциональна давлению.
Среднее эффективное сечение для воздуха (смеси газов см. таблицу 1.1) составляет σ ~ 62,5×10^–16 см2. Тогда < l > = 4,5×10^-3/p, где p (торр), < l> (см). Длина свободного пробега молекул воздуха при атмосферном давлении 760 торр и температуре 273 К (нормальные условия) соответственно < l > = 6×10^-6 см = 60 нм. Аналогичные параметры для других газов приведены в приложении 2.
Модель упругих шариков удовлетворительно выполняется для описания упругого взаимодействия медленных нейтральных молекул. При взаимодействии заряженных частиц с молекулами и при больших энергиях взаимодействующих частиц формула (1.30) не справедлива, а сечение зависит от энергии частиц. Однако полученная формула (1.31) имеет более широкую область применимости. Для описания взаимодействия произвольных частиц вводят понятие эффективного сечения σ(υ), которое в общем случае зависит от относительной скорости сталкивающихся частиц υ. Эффективное сечение либо рассчитывают теоретически на основании известного потенциала взаимодействия частиц, либо измеряют экспериментально, например, определяя ослабление пучка частиц в среде и вычисляя длину свободного пробега по формуле (1.27) или измеряя значение вязкости газов (взаимосвязь сечений и вязкости газов будет рассмотрена в следующих главах).
Если частица может взаимодействовать со средой по нескольким каналам, например, упруго рассеяться или ионизовать атом среды, то говорят об эффективном сечении определенного процесса σ_i, где i — порядковый номер процесса. Полное сечение, определяющее длину свободного пробега, задается очевидной формулой . При каждом столкновении вероятность Pi взаимодействия по определенному каналу есть

.                                    (1.34)

Примеры сечений ионизации и возбуждения различных газов электронным ударом, а также упругие сечения приведены в приложении 3.