Давление газов
Под давлением газа понимают средний импульс, предаваемый единице площади стенки сосуда молекулами газа в единицу времени. Рассмотрим плоскую стенку сосуда, в который помещен газ. Предположим также, что молекулы газа не прилипают к стенке, а упруго отражаются. Выберем ось x перпендикулярно стенке сосуда, а оси y и z — произвольно в перпендикулярной плоскости.
Будем считать стенку бесконечно тяжелой по сравнению с массой молекулы, тогда изменение импульса молекулы Dp, налетающей на стенку со скоростьюυ x вдоль оси x (y и z компоненты произвольны), составит
где m — масса молекулы.
Определим число молекул соударяющихся со стенкой сосуда площадью S в единицу времени. Рассмотрим множество молекул с проекцией скорости υ x. За время t до стенки долетят только молекулы, находящиеся на расстоянии менее υ xt, то есть в слое объемом Sυ xt. Здесь мы предполагаем, что молекулы не сталкиваются друг с другом. Для выполнения этого предположения необходимо выбрать t так, чтобы υ xt было меньше длины свободного пробега молекул между столкновениями. Согласно (1.12) концентрация молекул, имеющих скорости от υ x до dυ x, определяется выражением
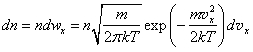 . (1.21)
. (1.21)
Таким образом, для числа молекул, сталкивающихся со стенкой площади S за время t, можно написать:
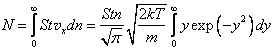 ,
,
а число молекул, сталкивающихся с единицей поверхности стенки в единицу времени соответственно:
С учетом (1.20) и (1.21) для давления получим
Важно отметить, что использование для определения давления выражения (1.23) и подстановка в (1.20) среднего значения проекции скорости не являются корректными. В конечном результате это приведет к ошибке в числовом коэффициенте формулы (1.24) в π раз.
Уравнение (1.24) известно под названием уравнение газового состояния. Его можно записать в форме, называемой законом Менделеева–Клапейрона
где V — объем газа,  — количество молей газа, NA = 6,02×1023 моль-1 — число Авогадро (количество молекул в одном моле вещества),R = kNA = 8,31 Дж×(K×моль)-1. Из уравнения (1.25) следует, что при нормальных условиях (давление 105 Па, температура 273 К) один моль идеального газа занимает 22,4 л.
— количество молей газа, NA = 6,02×1023 моль-1 — число Авогадро (количество молекул в одном моле вещества),R = kNA = 8,31 Дж×(K×моль)-1. Из уравнения (1.25) следует, что при нормальных условиях (давление 105 Па, температура 273 К) один моль идеального газа занимает 22,4 л.
В вакуумной технике обычно приходится иметь дело со смесями газов. Например, воздух представляет собой смесь, состав которой описан в таблице 1.1.
Таблица 1.1
Состав сухого атмосферного воздуха
| Газ | Состав, % | Парциальное давление, Па (при p= 105 Па) | Масса молекулы ´1026, кг |
| N2 | 78,1 | 7,81·104 | 4,65 |
| O2 | 21 | 2,10·104 | 5,31 |
| Ar | 0,9 | 9·102 | 6,63 |
| CO2 | 0,03 | 30 | 7,31 |
| Ne | 1,8·10-3 | 1,8 | 3,35 |
| He | 5,2·10-4 | 5,2·10-1 | 0,66 |
| CH4 | 2,0·10-4 | 2,0·10-1 | 2,65 |
| Kr | 1,0·10-4 | 1,0·10-1 | 13,9 |
| N2O | 5,0·10-5 | 5,0·10-2 | 7,3 |
| H2 | 5,0·10-5 | 5,0·10-2 | 0,33 |
| Xe | 9,0·10-6 | 9,0·10-3 | 21,8 |
Примечание.
В атмосфере имеются также пары воды. При 25 ºС и 50% влажности их парциальное давление составляет 1,2×103 Па.
Для смеси газов справедлив закон Дальтона: общее давление смеси химически невзаимодействующих газов равно сумме парциальных давлений компонентов смеси.
Единицей давления в системе СИ является 1 Па (Паскаль). Это давление, создаваемое при воздействии силы 1 Н на площадь 1 м2. Наиболее распространённой внесистемной единицей давления в вакуумной технике является миллиметр ртутного столба (торр). Под давлением газа 1 мм рт.ст. понимается давление, которое создаёт столбик ртути высотой 1 мм при условии, что плотность ртути равна 13595,1 кг/м3 (при T= 0 ºС), а земное ускорение соответствует нормальному (9,80665 м/с2 на широте 45º): 1 мм рт. ст. = 133,3 Н/м2. Соотношение между различными единицами давления даны в табл. 1.2.
Таблица 1.2
Соотношения между единицами давления
| Единицы давления | 1 Па (Н/м2) | 1 мм рт. ст. = 1 торр | 1 дин/см2 | 1 атм (физ.) | 1 кгс/см2 |
| 1 Па (1 Н/м2) | 1 | 7,5×10–3 | 10 | 9,87×10–6 | 1,02×10–5 |
| 1 мм рт.ст., (1 торр) | 1,33×102 | 1 | 1,33×103 | 1,32×10–3 | 1,36×10–3 |
| 1 дин/см2 | 0,1 | 7,5×10–4 | 1 | 9,87×10–7 | 1,02×10–6 |
| 1 атм.(физ.) | 1,01×105 | 760 | 1,01×106 | 1 | 1,03 |
| 1 кгс/см2 | 9,8×104 | 735,56 | 9,8´105 | 0,968 | 1 |
