§ 3.2.1. Перенос теплоты в вакууме
Теплопередача в разреженных газах может происходить за счет конвекции,теплопроводности и излучения.
При низком вакууме конвективный теплообмен играет важную роль. Перенос теплоты конвекцией от поверхности нити, нагретой до температуры Тп, к стенкам вакуумной камеры, имеющим температуру Т, описывается уравнением
где а — коэффициент теплообмена; А — площадь поверхности нити. При свободной конвекции из-за силового воздействия гравитационного поля на газ, имеющий различную плотность вследствие температурных градиентов, коэффициент теплообмена

где а — экспериментальный коэффициент, зависящий от материала и формы поверхности.
Коэффициент теплообмена в условиях вынужденной конвекции при поперечном обтекании нити для воздуха

где К — коэффициент теплопроводности газа; d — характерный размер (диаметр нити); Nu=k1Re*k2— критерий Нуссельта; Re= = vrdp/n — критерий Рейнольдса; vr — скорость газового потока; k1 и k2 — константы, зависящие от числа Re: k1 = 0,45; k2=0,5 при Re<103 и k1 = 0,245; k2=0,6 при Re>103.
Теплопроводность газа в качестве явления переноса при низком вакууме можно рассматривать аналогично вязкости газа. Вместо количества движения в этом случае переносится энергия молекул газа. Количество теплоты, отнесенное к одной молекуле газа,

где сv — теплоемкость газа при постоянном объеме; m — масса молекулы газа; Т—абсолютная температура.
Если концентрация газа п постоянна, то аналогично (3.1) можно записать выражение для теплового потока:
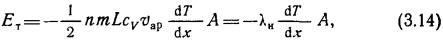
где λн — коэффициент теплопроводности газа при низком вакууме:
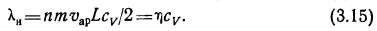
Таким образом, коэффициент теплопроводности газа равен произведению коэффициента динамической вязкости на удельную теплоемкость газа при постоянном объеме. Для расчета cv можно использовать выражение

где v=Cp/cv — отношение теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме (для одноатомных газов v=1,66; для двухатомных v=1,4; для трехатомных v=1,3; k — постоянная Больцмана; m — масса молекулы газа.
Молекулярно-кинетическая теория, используя функции распределения скоростей и длин свободного пути молекул газа, дает для коэффициента теплопроводности более точное выражение
![]()
отличающееся не более чем на 20% от значения, даваемого выражением (3.15).
Характер зависимости коэффициента теплопроводности и коэффициента динамической вязкости газа при низком вакууме от температуры и давления идентичен.
