§ 2.5. Растворимость газов в твердых телах

Концентрация газов, растворенных в твердом теле, зависит от его температуры, давления и типа кристаллической решетки. В металлах, для которых характерна гомополярная металлическая связь между электроположительными атомами, зависимость растворимости от давления и температуры имеет следующий вид:

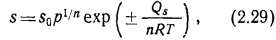
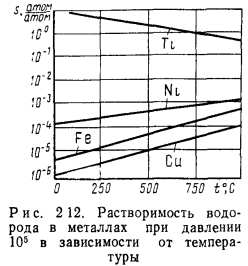
Рис. 2 12. Растворимость водорода в металлах при давлении 105 в зависимости от температуры

где п — число атомов в молекуле газа; Q_s — энергия активации при растворении; s₀ — постоянный коэффициент.

Знак «+» в формуле (2.29) характерен для газов, образующих с металлом химическое соединение, а знак «—» — для газов, образующих истинные растворы. Растворимость газов, образующих истинные растворы, с повышением температуры возрастает (Н₂ в Си, Fe и Ni), а образующих химические соединения — уменьшается (Н₂ в Ti). Растворимость s, показанная на рис. 2.12, рассчитывается как отношение числа атомов водорода к числу атомов металла. Отметим также, что растворимость водорода в Ti значительно больше, чем в Ni, Fe и Си.

Зависимость растворимости газов в металлах от давления представляет собой степенную функцию с показателем степени 1/я. Это связано с тем, что газы растворяются в металлах в атомарном состоянии и перед растворением происходит диссоциация молекул на атомы. Например, для кислорода /г—2, а реакция диссоциации имеет вид О₂↔0+0.

По закону действующих масс, константа равновесия такой реакции Кс=Р₀₂/Р_а2\ Р_о и р₀₂—давления атомарного и молекулярного кислорода.

Очевидно, что

Растворимость газов в металлах пропорциональна давлению диссоциированного газа. Для двухатомных молекул это равносильно пропорциональности корню квадратному из давления газа над поверхностью металла.

В неметаллах, атомы кристаллической решетки которых связаны между собой ионной или ковалентной связью, растворение газов происходит в молекулярном состоянии. Образуются истинные растворы, и зависимость растворимости газов от температуры и давления имеет вид

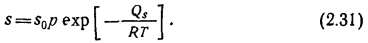
Значения постоянных s₀ и Q_s, характеризующих растворимость основных газов в металлах и неметаллах, и значения растворимости 5 приведены в табл. 2.8.

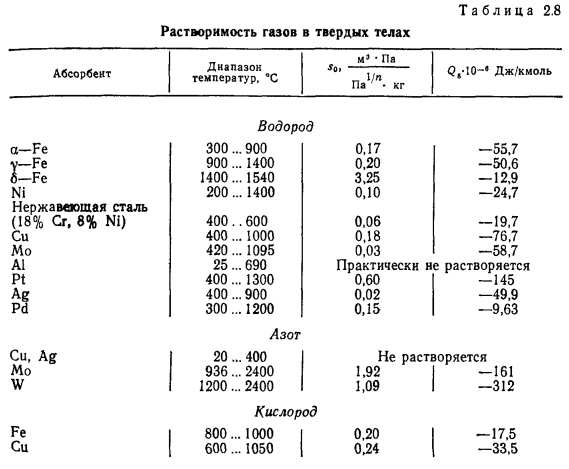
Абсорбционный процесс растворения газов в твердых телах осуществляется за счет диффузии молекул газа в кристаллическую решетку или по границам зерен. Диффузионный поток пропорционален градиенту концентрации. Так как для стационарного газового потока через стенку толщиной 2h градиент концентрации ds/dx=(s1-s2)/(2h), то

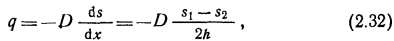
где q — число молекул, проходящих в единицу времени через единицу площади поперечного сечения в направлении оси х; D — коэффициент диффузии; S_iи S₂ — концентрации газа на границах стенки.

При повышении температуры коэффициент D сильно возрастает:

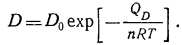
Здесь Q_D — энергия активации при диффузии; п — число атомов в молекуле газа для металлов, для неметаллов и=1; Do — коэффициент пропорциональности, не зависящий от температуры.

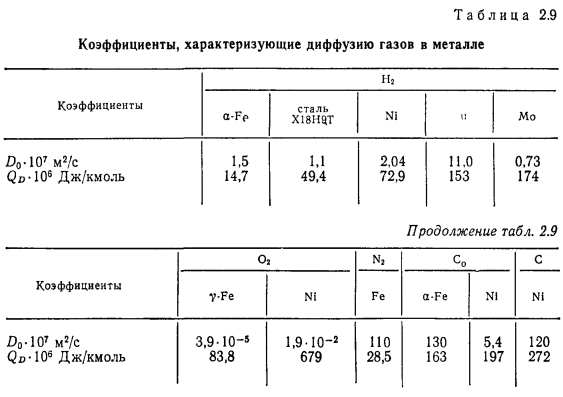
Значения Do и QD при диффузии газов в конструкционных материалах, приведенные в табл. 2.9, нужно рассматривать как приближенные в связи с тем, что на них влияют внутренние напряжения в материале. В тех случаях, когда диффузия происходит в основном по границам зерен и дефектам упаковки, необходимо дополнительно учитывать характер механической обработки, размеры и ориентацию кристаллов.

Подставляя в (2.32) выражение для D и s из (2.29), получим выражение для газопроницаемости металлов

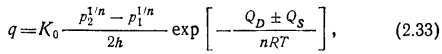
где K_o=D_oS_o — константа проницаемости.

Если градиент концентрации изменяется во времени, то в единице объема твердого тела происходит изменение концентрации вещества, описываемое дифференциальным уравнением нестационарной диффузии.