§ 2.4.2. Вывод уравнения БЭТ
Рассмотрим вывод уравнения (2.17). Условие адсорбционного равновесия для многослойной адсорбции (рис. 2.8) запишем в виде равенства скоростей конденсации в предыдущем адсорбционном слое и испарения в последующем слое:

Удельная скорость конденсации молекул в i-слое

где ft — вероятность конденсации молекул в i-слое, Nq — число молекул, ударяющихся в единицу времени о единицу поверхности. Воспользовавшись выражениями (1.14) и (1.18), перепишем (2.21) в виде

Удельная скорость испарения молекул

где а, — количество молекул, адсорбированных на единице поверхности; таi — время адсорбции молекул в i-слое.
С учетом выражения для времени адсорбции (2.3) уравнение (2.23) перепишем в виде:
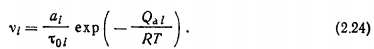
Согласно сделанным ранее допущениям, минимальное время адсорбции и вероятность конденсаций постоянны для всех слоев, т. е. T01=T02=…Тоi =...=То, a f1=f2= ...=fi=... =f. Тогда условие (2.20) с учетом уравнений (2.22) и (2.24) можно представить в виде системы уравнений:
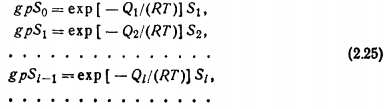
Здесь р — давление газа; Q, — теплота адсорбции в i-слое; S0, S1, ..., Si — величины свободных поверхностей адсорбента в соответствующем индексу слое; g — постоянный коэффициент.
В соответствии со сделанными допущениями Q1 = Qa; Q2=Q3= ... =Qi= ...=Е, где Е — теплота конденсации. Вводя эти упрощения, перепишем систему (2.25) в виде
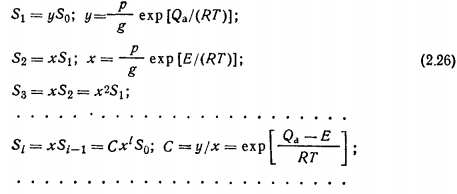
Полная поверхность адсорбента
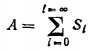
а количество адсорбированного вещества
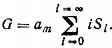
Удельное количество поглощенного газа определяется как
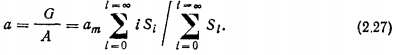
Если учесть, что
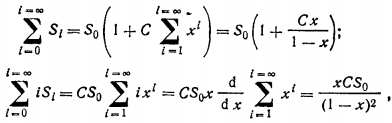
то после преобразований выражение (2.27) можно привести к виду
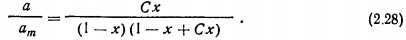
При давлении р, равном давлению насыщенных паров рт, на свободной поверхности может образоваться бесконечно большое число слоев. При этом Рт/g(ехр (E/RT) = 1, тогда х=р/рт. Подставляя полученное для х выражение в (2.28), получим уравнение полимолекулярной адсорбции
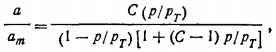
что совпадает с уравнением (2.17).
