§ 1.4.1. Распределение молекул газа по скоростям

При соударениях друг с другом или со стенками вакуумной камеры молекулы газа изменяют свои скорости как по величине, так и по направлению. Пользуясь гипотезами о существовании стационарного распределения молекул по скоростям и об изотропности пространства газовых молекул, а также учитывая, что. согласно (1.11), среднеквадратичная скорость V K_B = V₃kT/m, Максвелл получил функцию распределения молекул по скоростям:  

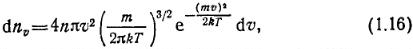
где dn v число молекул, скорости которых заключены в пределах от v до v+dv.

Скорость, при которой наблюдается максимум функции распределения, называется наиболее вероятной скоростью:

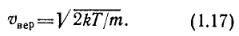
  Если ввести обозначение С=v/v_вep, то формулу (1.16) можно переписать так:  

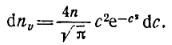
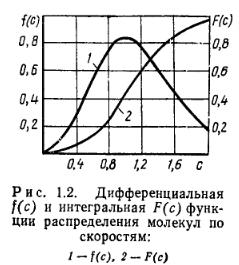
  Безразмерные функции f (с) = dnv/ (dne) и F (с)= f (с) de представлены на рис, 1.2. Функция Р(е) численно равна доле общего числа молекул, скорости которых не превышают с.  

В вакуумных расчетах часто используют скорости:

Среднеарифметическую:

среднеквадратичную

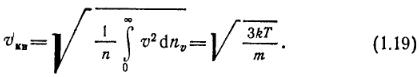
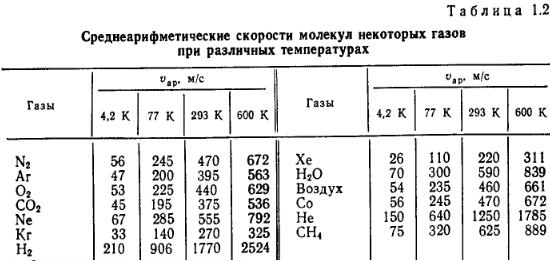
Соотношение между скоростями v_вер, v_ар и v_кв равно 1: 1,128:1,225, Так, указанные скорости для молекул азота при О^ОС составляют и в_е р=402 м/с, и а_р=453 м/с, и к_в =492 м/с. Среднеарифметические скорости молекул некоторых газов при различных температурах приведены в табло 1.2.  

  Согласно (1.14), для воздуха при Т=З00 К и М=29 кг/кмоль при атмосферном давлении поток газовых молекул N =29*10 ²³ см^-2c^-1, а из (1.15) объем молекул, ударяющихся единицу поверхности в единицу времени, V_q=11,6.103 м³ /(с см ^\2).  

Преобразуя (1.16), получим функцию распределения молекул по энергиям:

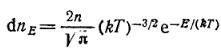
Здесь E= mv_кв 2/2 энергия f(x) поступательного движения молекулы; dnE число молекул, энергия которых лежит в интервале от Е до Е +dE. Вводя переменную х=Е/ (kT), получим

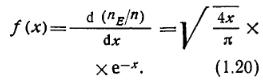
Интегральная кривая, представляющая собой долю молекул газа, энергия которых меньше Е, определяется функцией

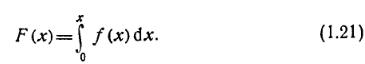
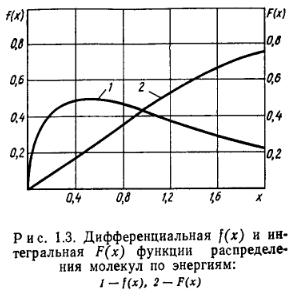
  На рис, 1,3 в безразмерной форме представлены графики функций (1,20) и (1,21), Максимум дифференциальной кривой соответствует наиболее вероятной энергии Е_вер=0,5 kT. Расчет среднеарифметического значения энергии молекул дает Е_ар= 1,5 kT,  

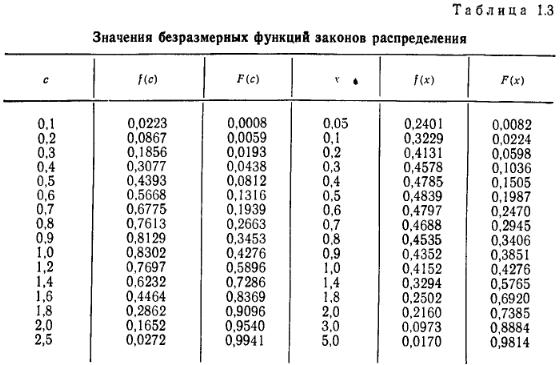
Наиболее важные значения безразмерных функций даны в табл. 1.3.