§ 1.2. Газовые законы
Если в объеме находится смесь из К химически не взаимодействующих газов, то для определения давления смеси Рем необходимо подсчитать сумму:
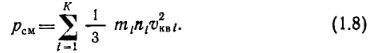
Сравнивая (1.7) и (1.8), можно записать:

Последнее выражение известно под названием закона Дальтона и формулируется следующим образом: общее давление смеси химически не взаимодействующих газов равно сумме парциальных давлений компонентов смеси.
Воспользовавшись определением температуры как величины, пропорциональной средней кинетической энергии молекул газа, можно записать mV 2 KB2/=cT, где с – постоянная, Тогда уравнение (1,7) для расчета давления газа можно представить в виде р=2/3ncT, Если обозначить k=2c/3, то

а средняя кинетическая энергия молекул

Уравнение (1.10) известно под названием уравнения газового состояния. Оно связывает между собой три основных параметра состояния газа: давление, молекулярную концентрацию и температуру.
Постоянная k называется постоянной Больцмана, и ее экспериментальное значение равно 1,38.102З Дж/К
Уравнение (1.10) можно представить также в другой записи:
![]()
где М молекулярная масса газа; V объем газа; Г универсальная газовая постоянная, R=kNa=8,31.10 3 Дж/(Г,моль), Na число Авогадро, Na =М/m=6,02, 1026кмоль-1,
Следствием (1.10) или (1,12) является то, что при постоянной массе и неизменном давлении объем газа пропорционален его абсолютной температуре (закон Гей-Люсака). Если же постоянны масса газа и его объем, то давление газа пропорционально его абсолютной температуре (закон Шарля). При постоянных массе и температуре газа произведение его давления на объем остается неизменным (закон Бойля-Мариотта). При постоянном давлении и температуре газа молекулярная концентрация не зависит от рода газа (закон Авогадро).
