§ 1.1.2. Условия равновесия
Каждой адсорбированной молекуле при этом соответствует одна десорбированная молекула с противоположным направлением вектора скорости. Таким образом, суммарное изменение количества движения адсорбированной и десорбированной молекул ∆K=2mv cos 8.
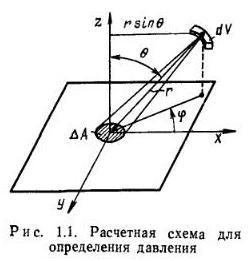
Согласно второму закону Ньютона, давление молекулы на поверхность твердого тела центра dV видна площадка ∆А:
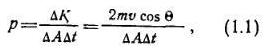
где ∆.А — площадь поверхности; At — время взаимодействия молекулы с поверхностью.
Число молекул в элементарном объеме &V, движущихся в направлении &А, с учетом постулата об отсутствии преимущественных на правлений пропорционально телесному углу dw, под которым из центра dw видна площадка ∆А:

Телесный угол

где r — расстояние между поверхностью и выделенным объемом (рис. 1.1.).
Для объема dV в полярной системе координат справедливо выражение:
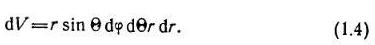
Давление газа на поверхность твердого тела найдем интегрированием по объему полусферы, из которой молекулы достигают поверхности за время ∆t, с радиусом R =v∆t.
С учетом выражения (1.1)
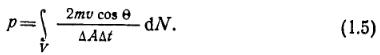
Подставляя (1.2), (1.3), (1.4) в (1.5), получим:

Согласно принятым постулатам, существует распределение молекул по скоростям, поэтому в (1.6) вместо постоянной введем среднеквадратичную скорость молекул.
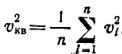
Тогда уравнение для расчета давления газа примет вид

Учитывая, что плотность газа р=nm, выражение (1.7) можно переписать как
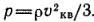
Условия равновесия, использованные при выводе уравнения (1.7), могут не выполняться. Примером является конденсирующая поверхность, с которой из-за очень большого времени адсорбции не происходит десорбции молекул газа. Тело, вылетевшее в космическое пространство из земной атмосферы, десорбирует с поверхности молекулы газа. Количеством же молекул, ударяющихся о поверхность этого тела, можно пренебречь. Для точного расчета давления газа на поверхности твердого тела нужно знать соотношение потоков падающих и вылетающих молекул газа.
